Números reales (R)
Incluyen todos los números que pueden representarse en una línea recta continua, es decir, poseen una ubicación definida en la recta numérica.
Clasificación de los números reales
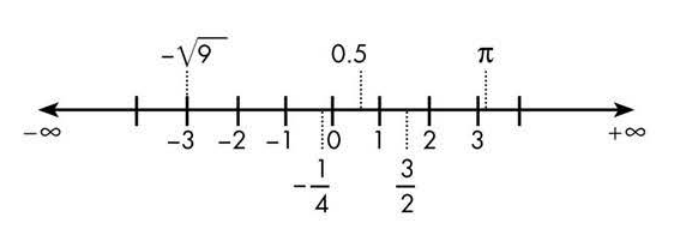
Números Naturales (N)
Son los números que usamos habitualmente para contar objetos. Su conjunto comienza desde el uno y continúa indefinidamente:
Ejemplos:
N = {1 ,2 ,3 ,4 , ...}
Números primos
Estos números solo pueden dividirse de manera exacta entre sí mismos y el uno.
Ejemplos:
{2 ,3 ,5 , 7, 11, 13, 17, 19,...}
Números compuestos
Son aquellos que pueden dividirse exactamente por más de dos números distintos.
Ejemplos comunes son:
{4, 6, 8, 9, 10, 12, …}
Números enteros (Z)
Este conjunto incluye tanto los números positivos como sus opuestos negativos, además del cero:
Ejemplos:
Z = = {…, -3, -2, -1, 0, 1, 2, 3, …}
Números racionales (Q)
Son aquellos que pueden expresarse como el cociente de dos enteros, donde el denominador no es cero. En otras palabras, son fracciones de la forma p/q, con p y q pertenecientes a los enteros y q ≠ 0.
Ejemplos:
Las fracciones comunes pueden organizarse en dos categorías principales, según su valor con respecto a la unidad.
Fracción propia
Es aquella cuyo numerador es menor que el denominador, por lo tanto, representa una cantidad menor que uno.
Ejemplos:
- ¹⁄₂, ³⁄₄, ⁵⁄₈
Fracción impropia
En este tipo de fracción, el numerador es igual o mayor que el denominador, por lo que su valor es igual o superior a uno.
Ejemplos:
- ⁴⁄₄, ⁷⁄₅, ⁹⁄₃
Números irracionales (Q')
Son todos aquellos números en los que su parte decimal se conforma de una serie infinita de dígitos, pero no existe periodo y por lo regular son resultado de raíces no exactas
Ejemplos:
\( π, \sqrt{2}, \frac{π}{2}, -\frac{\sqrt{3}}{4} \)
Números reales y sus propiedades de orden
Los números reales cumplen con ciertas reglas básicas que permiten establecer comparaciones entre ellos.
Estas reglas, llamadas postulados de orden, se detallan a continuación:
1. Tricotomía
Para cualquier par de números reales a y b, solo puede cumplirse una de las siguientes tres condiciones:
- -a > b
- -a > b
- -a = b
Es decir, entre dos números reales siempre existe una única relación de orden.
2. Transitividad
Si un número real es mayor que un segundo, y este segundo es mayor que un tercero,
entonces el primero también es mayor que el tercero.
Si a > b y b > c, entonces a > c
3. Propiedad aditiva del orden
Si un número real es mayor que otro, entonces al sumar la misma cantidad a ambos, la relación de orden se mantiene.
Si a > b, entonces a + c > b + c
4. Propiedad multiplicativa del orden
Multiplicar ambos lados de una desigualdad por un número positivo conserva el orden; si se multiplica por un número negativo, el orden se invierte:
- Si a > b y c > 0, entonces ac > bc
- Si a > b y c < 0, entonces ac < bc
Propiedades fundamentales de los números reales
Dados a, b y c pertenecientes al conjunto de los números reales R, se verifican las siguientes propiedades (operativas y algebraicas):
| Propiedad | Adición | Multiplicación |
|---|---|---|
| Cerradura | a + b ∈ R | a · b ∈ R |
| Conmutativa | a + b = b + a | a · b = b · a |
| Asociativa | a + (b + c) = (a + b) + c | a · (b · c) = (a · b) · c |
| Distributiva | a(b +c) = ab +ac | a(b +c) = ab +ac |
| Neutro | a + 0 = a | a · 1 = a |
| Inverso | a + (-a) = 0 | a · (1/n) = 1 |
Suma y resta
Con números enteros
Cuando los signos son iguales
Si ambos números tienen el mismo signo, se suman sus valores absolutos y se conserva el signo común.
Ejemplos:
- -(+4) + (+6) =+ 10
- -(−3) + (−5) =− 8
- -(−7) + (−2) =− 9
Cuando los signos son diferentes
Se realiza la resta entre los valores absolutos de los números y el resultado toma el signo del número con mayor valor absoluto.
Ejemplos:
- - (+8)+(−5)=+3
- - (−9)+(+4)=−5
- - (+6)−(+10)=−4
Signos de agrupación
Se utilizan para organizar y dar prioridad a ciertas operaciones dentro de una expresión matemática. Los símbolos más comunes son:
- Paréntesis: ( )
- Corchetes: [ ]
- Llaves: { }
- Vínculo o barra de fracción: ―
Cómo operar con signos de agrupación
Para eliminar un signo de agrupación, se aplica la operación indicada por el número o signo que lo precede.
Si hay varios niveles de agrupación, deben resolverse en orden, comenzando desde los signos más internos hacia los externos.
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Al simplificar la expresión -(-4 + 6) se obtiene:
2. El resultado de simplificar -2 + [6 - (4 - 1)] es:
3. La simplificación de -2 + {6 - 2 [5 - 1 + 2(3 - 6)] + 4} es:
4. Al simplificar la expresión 4 - (-1 + 3 - (6 - 9 + (2 - 7) - (5 - 8)) - 2), se obtiene:
Con números racionales
Máximo Común Divisor (MCD)
El MCD es el número más grande que divide de manera exacta a dos o más números, es decir, sin dejar residuo. Se trata del mayor valor que todos los números considerados tienen como divisor en común.
Ejemplo:
Para los números 12 y 18:
- Los divisores de 12 son: 1, 2, 3, 4, 6, 12
- Los divisores de 18 son: 1, 2, 3, 6, 9, 18
- El mayor divisor común es: 6, por lo tanto, MCD(12, 18) = 6
Mínimo Común Multiplo (mcm)
El mcm es el número más pequeño, distinto de cero, que es múltiplo de dos o más números a la vez. Es decir, es el primer número que aparece en la lista de múltiplos de cada uno de ellos.
Ejemplo:
Para los números 4 y 6:
- Múltiplos de 4: 4, 8, 12, 16, 20, 24, …
- Múltiplos de 6: 6, 12, 18, 24, 30, …
- El múltiplo más pequeño que ambos comparten es 12, por lo tanto, mcm(4, 6) = 12
Fracciones comunes con denominadores iguales
Los numeradores se suman o se restan y se escribe el denominador en común.
Ejemplo:
- 2/7 + 8/7 + 3/7 = 2+8+3/7 = 13/7 = 1 6/7
- 5/3 + 7/3 - 10/3 = 5+7-10/3 = 2/3
- 11/4 - 7/4 = 11-7/4 = 4 = 1
Fracciones con denominadores distintos
Cuando se suman o restan fracciones que no tienen el mismo denominador, es necesario igualarlos antes de operar. Para ello, se sigue el siguiente procedimiento:
Se determina el mínimo común múltiplo (mcm) de los denominadores; este será el denominador común.
Cada fracción se convierte a una fracción equivalente con ese denominador común:
- Se divide el mcm entre el denominador original
- El resultado se multiplica por el numerador correspondiente.
Finalmente, se suman o restan los numeradores según indique la operación, manteniendo el denominador común.
Multiplicación y División
Con números enteros
Leyes de los signos
| Multiplicación | |||
|---|---|---|---|
| (+)(+) = + | (-)(-) = + | (+)(-) = - | (-)(+) = - |
| División | |||
|---|---|---|---|
| \( \frac{+}{+} \) = + | \( \frac{-}{-} \) = + | \( \frac{+}{-} \) = - | \( \frac{-}{+} \) = - |
Ejemplos:
- (-4)(3) = -12
- (-6)(-7) = 35
- (-2)(-6)(-7) = -84
- \( \frac{-76}{19} \) = -4
- \( \frac{(-12)(34)}{-4} = \frac{-36}{-4} \) = -4
- \( \frac{(-7)(6)(-15)}{(14)(-9)} = \frac{630}{-126} \) = -5
Con números racionales
Multiplicación
Para multiplicar fracciones, se multiplica directamente el numerador de la primera fracción por el numerador de la segunda, y el denominador por el denominador. Además, se aplican las reglas de los signos igual que en cualquier operación con números enteros.
Ejemplos:
En la razón ⅔ o 2 : 3, el 2 es el antecedente y el 3 el consecuente.
Ejemplos:
- \( (\frac{5}{6}) (\frac{2}{15}) = \frac{(5)(2)}{(6)(15)} = \frac{10}{90} = \frac{1}{9} \)
- (-3) \( (\frac{7}{2}) = \frac{(3)(1)}{(7)(12)} = -\frac{21}{12} = -\frac{7}{4} \)
- \( (2\frac{1}{4}) = \frac{(9)(4)}{(10)(21)} = \frac{(9)(10)}{(4)(21)} = \frac{90}{84} = \frac{15}{14} \)
División
Para dividir fracciones, se multiplica la primera fracción por el recíproco (inverso) de la segunda. Es decir, se invierte la segunda fracción y luego se realiza una multiplicación normal. También se aplican las leyes de los signos como en cualquier operación entre números con signos.
Ejemplos:
- \( (\frac{2}{3}) (\frac{4}{5}) = \frac{(2)(5)}{(3)(4)} = \frac{10}{12} = \frac{5}{6} \)
- 3 +\( (\frac{9}{7}) = \frac{3}{1} + \frac{9}{7} = -\frac{(3)(7)}{(1)(9)} = \frac{21}{9} = \frac{7}{3} \)
- 2 \( \frac{3}{5} + 1 \frac{1}{2} = \frac{13}{5} + \frac{3}{2} = \frac{(13)(2)}{(5)(3)} = \frac{26}{15} \)
División vertical de fracciones
Cuando la división de fracciones se presenta en forma vertical (como una fracción dividida por otra), se aplican los productos cruzados:
- Se multiplican los extremos (numerador de la primera por denominador de la segunda) para obtener el numerador del resultado.
- Se multiplican los medios (denominador de la primera por numerador de la segunda) para obtener el denominador.
Ejemplos:
- \( \frac{\frac{2}{3}}{\frac{5}{9}} = \frac{(2)(9)}{(3)(5)} = \frac{18}{15} = \frac{6}{5} \)
- \( \frac{2}{\frac{7}{2}} = \frac{\frac{3}{1}}{\frac{7}{2}} = \frac{6}{7} \)
- \( \frac{\frac{4}{15}}{8} = \frac{\frac{4}{15}}{\frac{8}{1}} = \frac{4}{120} = \frac{1}{30} \)
Fracciones complejas
Una fracción compleja es aquella que incluye otras fracciones dentro de su numerador, su denominador o en ambos. Es decir, se trata de expresiones que involucran operaciones entre fracciones anidadas.
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Al simplificar la siguiente expresión \( \frac{2 + \frac{4}{15}}{2 - \frac{1}{3}} \) se obtiene:
Solución: Se identifican las operaciones secundarias, las cuales serán las primeras en ser resueltas:
\( \frac{2 + \frac{4}{15}}{2 - \frac{1}{3}} = \frac{\frac{2}{1} + {\frac{1}{3}}} {\frac{2}{1} + {\frac{1}{3}}} = \frac{\frac{6 + 1}{3}} {\frac{6-1}{3}} = \frac{\frac{7}{3}} {\frac{5}{3}} = \frac{(3)(7)}{(3)(5)} =\frac{7}{5} \)
2. La simplificación de \( \left(1 +\frac{1}{1-\frac{1}{2}}\right) \) \( \left(1 -\frac{1}{1+\frac{1}{2}}\right) \) es:
Solución:
\( \left(1 +\frac{1}{1-\frac{1}{2}}\right) \) \( \left(1 -\frac{1}{1+\frac{1}{2}}\right) \) = \( \left(1 +\frac{1}{\frac{2-1}{2}}\right) \) \( \left(1 +\frac{1}{\frac{2+1}{2}}\right) = \left(1 +\frac{1}{\frac{1}{2}}\right) \) \( \left(1 +\frac{1}{\frac{3}{2}}\right) = (1 + 2) \left(1 -\frac{2}{3}\right) = (3) \left(\frac{1}{3}\right) = 1 \)
3. Al simplificar la expresión \( \frac{\frac{1}{2} + \frac{1}{3}} {\frac{1}{2} - \frac{1}{3}} \) se obtiene:
Solución:
\( \frac{\frac{1}{2} + \frac{1}{3}} {\frac{1}{2} - \frac{1}{3}} = \frac{\frac{3+2}{6}} {\frac{3-2}{6}} = \frac{\frac{5}{6}} {\frac{1}{6}} = \frac{(6)(5)}{(6)(1)} = \frac{30}{6} = 5\)
Problemas de aplicación:
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Para construir una barda se necesitan 300 ladrillos. Si cada hora se colocó \( \frac{1}{15} \) del total de ladrillos, ¿en cuántas horas se colocaron 225 ladrillos?
Solución:
1. Se determina el número de ladrillos colocados cada hora:
\( \frac{1}{15}\) (300) = 20 ladrillos
2. Para determinar el número de horas para colocar 225 ladrillos esta cantidad se divide por los 20 ladrillos, entonces:
\( \frac{225}{20}\) = \( \frac{45}{4}\) = 11 \( \frac{1}{4} \) h
2. Las dimensiones de un rectángulo son 12 x 20 cm, si el ancho se aumenta en su tercera parte y el largo en su cuarta parte. ¿Qué fracción representa el área inicial del área resultante?
Solución:
1. Se determinan las dimensiones del nuevo rectángulo:
El ancho se aumenta en su tercera parte: 12 + \( \frac{1}{3} \) (12) = 12 + 4 = 16 cm
El largo se aumenta en su cuarta parte: 20 + \( \frac{1}{4} \) (20) = 20 + 5 = 25 cm
2. Las dimensiones del nuevo rectángulo son: 16 x 25 cm y su área es de 400 cm cuadrados.
El área del rectángulo con dimensiones 12 x 20 cm es de 240 cm cuadrados.
3. La fracción que representa el área inicial del área resultante es:
\( \frac{240}{400} \) = \( \frac{24}{40} \) = \( \frac{3}{5} \)
3. Un contenedor de agua de 500 litros está lleno hasta un cuarto de su capacidad total. Si se agregan al contenedor 300 litros, ¿qué parte del total de agua del contenedor se debe agregar para llenarlo?
Solución:
1. Se determinan los litros que tiene el contenedor, si está lleno hasta un cuarto de su capacidad total, entonces
\( \frac{1}{4} \) (500) = 125 L
2. Luego, se agregan 300 L, por tanto, tendrá 425 L. Para que el contenedor se llene le faltan 75 L, y esta cantidad en fracción representa:
\( \frac{75}{500} \) = \( \frac{15}{100} \) = \( \frac{3}{20} \) del total
Razones y proporciones
Razón
Una razón representa la comparación entre dos cantidades mediante una división. En esta expresión, el número que va en el numerador se llama antecedente, y el que está en el denominador se llama consecuente.
Ejemplos:
En la razón ⅔ o 2 : 3, el 2 es el antecedente y el 3 el consecuente.
Proporción
Una proporción es una igualdad entre dos razones. Expresa que dos relaciones son equivalentes.
Se puede representar como:
a/b = c/d o también como a : b :: c : d
Y se lee: "a es a b, como c es a d".
Términos de una proporción
En una proporción escrita como \( \frac{a}{b} = \frac{c}{d} \), cada uno de los elementos tiene un nombre específico:
- Extremos: son los valores que se encuentran en los extremos de la igualdad, es decir, a y d.
- Medios: son los valores ubicados en el centro de la proporción, es decir, b y c.
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. El valor de x en la proporción \( \frac{x}{3} = \frac{12}{4} \) es:
Solución: En toda proporción el valor de un extremo equivale al producto de los medios dividido por el extremo restante.
\( \frac{x}{3} = \frac{12}{4} \) → \( x = \frac{(3)(2)}{4} = \frac{36}{4} \) = 9
2. El valor de y en la proporción \( \frac{7}{x} = \frac{10}{2} \) es:
Solución: En toda proporción el valor de un medio equivale al producto de los extremos dividido por el medio restante.
\( \frac{7}{y} = \frac{10}{2} \) → \( y = \frac{(7)(2)}{10} = \frac{14}{10} = \frac{7}{5} \)
Proporción directa (Regla de tres directa)
Se dice que dos cantidades están en proporción directa cuando al aumentar una, la otra también aumenta en la misma proporción; y si una disminuye, la otra también lo hace proporcionalmente.
Definición:
Si m se relaciona con n de la misma manera que c con d, entonces:
\( \frac{m}{n} = \frac{c}{d} \)
Este principio es la base de la regla de tres directa, utilizada para resolver problemas donde intervienen cantidades que mantienen una relación proporcional.
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Se compran 25 dulces con $12.00, ¿cuántos dulces se pueden comprar con $36.00?
Solución: La proporción es directa, ya que con más dinero se compra un mayor número de dulces. Se establece la proporción: 25 dulces es a $12.00 como x es a $36.00, entonces:
\( \frac{25}{12} = \frac{x}{36} \) → \( x = \frac{(25)(36)}{12} = \frac{900}{12} \) = 75
2. Un comerciante vende un artículo en $112 y gana 40% sobre el costo del artículo, ¿cuál es el costo de dicho artículo?
Solución: Sea x el costo del artículo que representa el 100% y $112.00 el 140%, entonces:
\( \frac{x}{100} = \frac{112}{140} \) → \( x = \frac{(12)(100)}{140} = \frac{11200}{140} \) = 80.00
Proporción inversa (Regla de tres inversa)
Se dice que dos cantidades están en proporción inversa cuando, al aumentar una, la otra disminuye en la misma proporción, y viceversa. Esto significa que su producto permanece constante.
Definición:
Si m se relaciona con n de forma inversa, y c con d, entonces:
m * n = c * d
Este tipo de relación es útil en situaciones donde el cambio en una cantidad provoca el efecto contrario en otra, como en casos de velocidad y tiempo, o número de trabajadores y duración de una tarea.
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Un automóvil viaja a razón de 60 km/h y tarda 3 horas en ir de una ciudad a otra. ¿A qué velocidad debe regresar para cubrir dicha distancia en 2 h?
Solución: La proporción es inversa, ya que a mayor velocidad menos tiempo tardará en recorrer cierta distancia.
Se establece la proporción: 60kmh es a 3 horas como x es a 2 h, entonces:
\( (60)(3) = 2x → x = \frac{(60)(30)}{2} = \frac{180}{2} = 90 \frac{km}{h} \)
Raíces y potencias
Potencia
Una potencia es una forma abreviada de escribir un producto repetido de un mismo número. Se compone de una base que se multiplica por sí misma tantas veces como lo indica el exponente.
Se representa así: an
Donde:
a es la base (el número que se repite)
n es el exponente (el número de veces que se multiplica la base)
Ejemplos:
- \( 3^{4} \) = (3)(3)(3)(3) = 81
- \( \left(\frac{2}{7} \right)^{3} = \left(\frac{2}{7} \right) \left(\frac{2}{7} \right) \left(\frac{2}{7} \right) = \frac{8}{343} \)
- \( -5^{3} \) = (5)(5)(5) = -125
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. El resultado de \( \frac{2^{3} * 5^{2}}{2^{3}} \) es:
Solución:
\( \frac{2^{3} * 2^{5}}{2^{2}} = \frac{2^{3+5}}{2^{2}} = 2^{8-2} = 2^{6}\)
2. Al simplificar la expresión \( \frac{3^{4}}{3^{2}} \left(\frac{3^{6}}{3^{7}} \right)^{\frac{1}{3}} \) se obtiene:
Solución:
\( \left(\frac{3^{4}}{3^{2}}\right)^{\frac{1}{3}} = \left(3^{4-7}\right)^{\frac{1}{3}} = \left(3^{-3}\right)^{\frac{1}{3}} = 3^{-3}{\frac{1}{3}} = 3^{\frac{-3}{3}} = 3^{-1} = \frac{1}{3}\)
Radicación
La radicación es una operación que permite encontrar un número que, al multiplicarse por sí mismo tantas veces como lo indica el índice, da como resultado el radicando.
Se representa con el símbolo de raíz: \(\sqrt[n]{a}\)
Ejemplo:
\(\sqrt[3]{27} = 3\) porque 3 x 3 x 3 = 27
Simplificación de radicales
Dado un radical de la forma \(\sqrt[n]{a} = 3\) expresarlo en su forma más sencilla.
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Una expresión equivalente a \(\sqrt[3]{54} \) es:
Solución: Se descompone 54 en sus factores primos:
\( 54 = 3 * 3 * 3 * 3 = 2 * 3^{3} \)
Por consiguiente, \( \sqrt[3]{54} = \sqrt[3]{2 * 3^{3}} = \sqrt[3]{2} * \sqrt[3]{2 * 3^{3}} = 3\sqrt[3]{2} \)
2. Al simplificar \(\sqrt[3]{128} \) se obtiene:
Solución: Se descompone el radicando en sus factores primos
\( 128 = 2^{7} \)
Luego, \( \sqrt[3]{128} = \sqrt[3]{2^{7}} = \sqrt[3]{2^{6} · 2} = \sqrt[3]{2^{6}} · \sqrt[3]{2} = 2^{2} · \sqrt[3]{2} = 4\sqrt[3]{2} \)
Suma y resta de radicales
Para sumar o restar radicales deben tener el mismo índice y el mismo radicando.
\( a\sqrt[n]{d} + b\sqrt[n]{d} - c\sqrt[n]{d} = (a + b - c) \sqrt[n]{d} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. El resultado de \( 2\sqrt{3} + 5\sqrt{3} - 3\sqrt{3} \) es
Solución: En la operación el índice y el radicando coinciden, entonces:
\( 2\sqrt{3} + 5\sqrt{3} - 3\sqrt{3} = (2 + 5 - 3)\sqrt{3} = 4\sqrt{3} \)
2. El resultado de \( \sqrt{18} - \sqrt{50} + \sqrt{98} \) es:
Solución: Para resolver la operación se realiza una sim plificación de radicales, porque los radican dos no son los mismos, entonces:
\( \sqrt{18} = \sqrt{3^{2} · 2} = \sqrt{3^{2}} · \sqrt{2} = 3\sqrt{2} ; \sqrt{50} = \sqrt{5^{2} · 2} = \sqrt{5^{2}} · \sqrt{2} = 5\sqrt{2} \)
\( \sqrt{98} = \sqrt{7^{2} · 2} = \sqrt{7^{2}} · \sqrt{2} = 7\sqrt{2} \)
Entonces: \( \sqrt{18} - \sqrt{50} + \sqrt{98} = 3\sqrt{2} - 5\sqrt{2} + 7\sqrt{2} = (3 - 5 + 7)\sqrt{2} = 5\sqrt{2} \)
Propiedades de los radicales
1) \( \sqrt[n]{a^{n}} = a \)
2) \( \sqrt[m]{a^{\frac{n}{m}}} = a^{\frac{n}{m}} \)
3) \( \sqrt[n]{a} · \sqrt[n]{b} = \sqrt[n]{ab} \)
4) \( \sqrt[n]{a^{a}} · \sqrt[m]{b} = \sqrt[nm]{a^{m} · a^{n}} \)
5) \( \sqrt[n]{\sqrt[m]{a}} = \sqrt[nm]{a} \)
6) \( \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}} \)
7) \( \frac{\sqrt[n]{a}}{\sqrt[m]{b}} = \sqrt[nm]{\frac{a^{m}}{b^{n}}} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Al simplificar la expresión \( \sqrt[3]{5^{6}} \) se obtiene:
Solución: Al aplicar \( \sqrt[m]{a^{n}} = a^{\frac{n}{m}} \) se obtiene \( \sqrt[3]{5^{6}} = 5^{\frac{6}{3}} = 5^{2} \)
2. Al simplificar \( \sqrt{\sqrt[3]{64}} \) se obtiene:
Solución: Al aplicar \( \sqrt[n]{\sqrt[m]{a}} = \sqrt[mn]{a} \) se obtiene \( \sqrt{\sqrt[3]{64}} = (2)(3)\sqrt{64} = \sqrt[6]{64} = \sqrt[6]{2^{6}} = 2 \)
Multiplicación de radicales
Con índices iguales
Se aplica la siguiente propiedad:
\( \sqrt[n]{a} · \sqrt[n]{b} = \sqrt[n]{ab} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Al realizar la multiplicación \( \sqrt{3} · \sqrt{2} \) se obtiene:
Solución:
\( \sqrt{3} · \sqrt{2} = \sqrt{(3)(2)} = \sqrt{6} \)
2. Al realizar la multiplicación \( \sqrt[3]{4} · \sqrt[3]{2} \) se obtiene:
Solución:
\( \sqrt[3]{4} · \sqrt[3]{2} = \sqrt[3]{(4)(2)} = \sqrt[3]{8} = \sqrt[3]{2^{3}} = 2 \) se obtiene \( \sqrt[3]{5^{6}} = 5^{\frac{6}{3}} = 5^{2} \)
Con índices diferentes
Se aplica la siguiente propiedad:
\( \sqrt[n]{a} · \sqrt[m]{b} = \sqrt[nm]{a^{m} · b^{n}} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. La simplificación de la multiplicación \( \sqrt[3]{4} · \sqrt{5} \) es:
Solución: Los índices de la s raíces son diferentes, por consiguiente, se aplica
\( \sqrt[n]{a} · \sqrt[m]{b} = \sqrt[nm]{a^{m}} \) entonces: \( \sqrt[3]{4} · \sqrt{5} = \sqrt[(3)(2)]{4^{2} · 5^{3}} = \sqrt[6]{16 · 125} = \sqrt[6]{2000} \)
2. Una expresión equivalente a \( \sqrt[4]{2} · \sqrt{2} \) es:
Solución: Se convierten los radicales a un índice común y se multiplican los radicandos:
\( \sqrt[4]{2} · \sqrt{2} = \sqrt[4]{2 · 2^{2}} = \sqrt[4]{2^{3}} = 2^{\frac{3}{4}} \)
División de radicales
Con índices iguales
Se aplica la siguiente propiedad:
\( \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. El resultado de \( \frac{\sqrt{15}}{\sqrt{3}} \) es:
Solución:
\( \frac{\sqrt{15}}{\sqrt{3}} = \sqrt{\frac{\sqrt{15}}{3}} = \sqrt{5} \)
2. El resultado de la división \( \frac{\sqrt[3]{48}}{\sqrt[3]{2}} \) es:
Solución:
\( \frac{\sqrt[3]{48}}{\sqrt[3]{2}} = \sqrt[3]{\frac{48}{2}} = \sqrt[3]{24} = \sqrt[3]{2^{3} · 3} = \sqrt[3]{2^{3}} · \sqrt[3]{3} = 2\sqrt[3]{3} \)
Con índices diferentes
Se aplica la siguiente propiedad:
\( \frac{\sqrt[n]{a}}{\sqrt[m]{b}} = \sqrt[nm]{\frac{a^{m}}{b^{n}}} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Una expresión equivalente a \( \frac{\sqrt{2}}{\sqrt[3]{2}} \) es:
Solución:Los índices de las raíces son diferentes, por tanto, se aplica \( \frac{\sqrt{2}}{\sqrt[3]{2}} \), entonces:
\( \frac{\sqrt{2}}{\sqrt[3]{2}} = \sqrt[2]{frac{\sqrt{2^{3}}}{2^{2}}} = \sqrt[6]{\frac{8}{4}} = \sqrt[6]{2} \)
2. El resultado de \( \frac{\sqrt{3}}{\sqrt[4]{3}} \) es:
Solución:
\( \frac{\sqrt{3}}{\sqrt[4]{3}} = \sqrt[4]{frac{\sqrt{3^{2}}}{3}} = \sqrt[4]{3} \)
Racionalización
Racionalizar es representar una fracción que contenga una raíz en el denominador, en otra fracción equivalente, cuyo denominador sea un número racional.
Racionalización de un denominador monomio
Dada una fracción de la forma \( \frac{c}{\sqrt[n]{a^{m}}} \) su racionalización se efectúa al multiplicar por el término \( \frac{n}{\sqrt[n]{a^{n-m}}}{\sqrt[n]{a^{n-m}}} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Al racionalizar la expresión \( \frac{1}{\sqrt{2}} \) se obtiene:
Solución: Para racionalizar la fracción \( \frac{1}{\sqrt{2}} \) se multiplica por \( \sqrt{2} \) tanto numerador como denominador.
\( \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} · \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{\sqrt{2^{2}}} = \frac{\sqrt{2}}{2} \)
2. Al racionalizar la expresión \( \frac{6}{\sqrt{3}} \) se obtiene:
Solución: La fracción se multiplica por \( \sqrt{3} \) tanto numerador como denominador.
\( \frac{6}{\sqrt{3}} = \frac{6}{\sqrt{3}} · \frac{\sqrt{3}}{\sqrt{3}} = \frac{6\sqrt{3}}{3} = 2\sqrt{3} \)
Racionalización de un denominador binomio
Para racionalizar una fracción con denominador binomio se multiplica por su conjugado
Conjugado de un binomio
Dado el binomio (a + b) su conjugado es el binomio (a- b) y viceversa, el producto de dos binomios conjugados da como resultado una diferencia de cuadrados.
\( (a + b)(a - b) = a^{2} - b^{2} \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Al racionalizar la expresión \( \frac{1}{3 + \sqrt{2}} \) se obtiene:
Solución: Se multiplica tanto denominador como numerador por \( 3 - \sqrt{2} \), entonces:
\( \frac{1}{3 + \sqrt{2}} = \frac{1}{3 + \sqrt{2}} · \frac{3 - \sqrt{2}}{3 - \sqrt{2}} = \frac{3 - \sqrt{2}}{\sqrt{(3)^{2} - (\sqrt{2})^{2}}} = \frac{3 - \sqrt{2}}{9 - 2} = \frac{3 - \sqrt{2}}{7} \)
2. Al racionalizar la expresión \( \frac{2}{4 - \sqrt{5}} \) se obtiene:
Solución:Se multiplica tanto numerador como denominador por \( 3 + \sqrt{5} \), entonces:
\( \frac{2}{4 - \sqrt{5}} = \frac{2}{4 - \sqrt{5}} · \frac{4 + \sqrt{5}}{4 + \sqrt{5}} = \frac{2(4+\sqrt{5})}{(4)^{2} - (\sqrt{5})^{2}} = \frac{2(4 + \sqrt{5})}{16 - 5} = \frac{2(4 + \sqrt{5})}{11} = \frac{8 + 2\sqrt{5}}{11} \)





