Números complejos
Números imaginarios
La unidad imaginaria se define como:
\( i = \sqrt{-1} \)
Ejemplos:
- \( \sqrt{-100} = \sqrt{(100)(-1)} = \sqrt{100} · \sqrt{-1} = 10i \)
- \( \sqrt{-12} = \sqrt{(4·3)(-1)} = \sqrt{4} · \sqrt{3} · \sqrt{-1} = 2\sqrt{3}·i = 12\sqrt{3i} \)
- \( \sqrt{\frac{-49}{4}} = \sqrt{\frac{49}{4}}· \sqrt{-1} = (\frac{7}{2})i \)
Suma y resta de números imaginarios
Se aplica la siguiente expresión:
\( ai + bi - ci = (a + b - c) i \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. El resultado de simplificar \( 3i−5i+9i \) es:
Solución:
\( 3i − 5i + 9i = (3−5+9)i = 7i \)
2. Al simplificar \( 6i + \frac{3}{2} - 2i \) se obtiene:
Solución:
\( 6i + \frac{3}{2}i - 2i = (6 - 2 + \frac{3}{2})i + (4 + \frac{3}{2})i = \frac{11}{2}i \)
Potencias de i
Son los resultados de elevar i a una potencia n.
\( i^{1} = i, i^{2} = -1, i^{3} = -i, i^{4} = 1, ... \)
A partir de \( i^{5} \), los resultados anteriores se repiten en el mismo orden.
Números complejos
Un número complejo es de la forma \( a + bi \), \( con a, b E R \)
Donde:
a: parte real b: parte imaginaria \( i = \sqrt{-1} \)
Los números complejos se representan de dos formas:
1) \( z = a + bi \) forma rectangular
2) \( z = (a,b) \) forma cartesiana
| Forma rectangular | Forma cartesiana |
|---|---|
| \( z_1 = 6 + 8i \) | \( z_1 = (6, -8) \) |
| \( z_2 = 4 + 5i \) | \( z_2 = (4, 5) \) |
| \( z_3 = -3 \) | \( z_3 = (-3, 0) \) |
| \( z_4 = 7i \) | \( z_4 = (0, -7) \) |
| \( z_5 = \frac{3}{5} - \frac{2}{5} \) | \( z_5 = (\frac{3}{5}, \frac{2}{5}) \) |
Gráfica de un número complejo
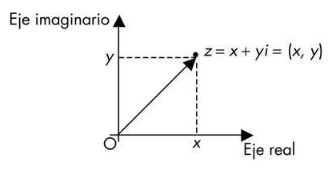
Un número complejo se puede ubicar en un plano cartesiano especial llamado plano complejo. En este sistema, el eje horizontal representa la parte real, y el eje vertical representa la parte imaginaria.
Si tenemos un número complejo expresado como: \( z = x + yi \)
- x corresponde a la parte real
- y es la parte imaginaria
La gráfica de \( z \) se representa como un punto en el plano complejo, localizado en la posición \( (x,y) \).
Ejemplo:
1. Trazar la gráfica del número complejo \( z = −2 + 5i \)
1. Se identifica la forma rectangular del número complejo.
2. En el plano complejo, se ubica el punto.
3. −2 sobre el eje real (hacia la izquierda)
4. 5 sobre el eje imaginario (hacia arriba)
5. Se marca el punto correspondiente a (−2,5), que representa gráficamente al número complejo z= −2 + 5i.
Magnitud de un número complejo
La magnitud (o módulo) de un número complejo representa la distancia entre el origen del plano complejo y el punto que representa al número en su forma rectangular.
Si se tiene un número complejo de la forma: z = a + bi
Donde a es la parte real y b la parte imaginaria, entonces su magnitud se calcula mediante la fórmula:
\( z = \sqrt{a^{2} + b^{2}} \)
Esta expresión se obtiene aplicando el teorema de Pitágoras, considerando que el número complejo forma un triángulo rectángulo en el plano complejo.
EJERCICIO
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. La magnitud de \( z = 3 + 4i \) es:
Solución:
1. Identificamos la parte real y la parte imaginaria: \( a = 3, b = 4 \)
2. Aplicamos la fórmula de la magnitud: \( |z| = \sqrt{a^{2} + b^{2}} \)
3. Sustituimos los valores: \( |z| = \sqrt{3^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} \)
4. Resultado: \( |z| = 5 \)
Operaciones con números complejos
Suma y resta
Para realizar operaciones entre números complejos, basta con sumar o restar sus partes reales e imaginarias por separado.
Sean dos números complejos:
\( z = a + bi y w = x + yi \)
Sean dos números complejos:
\( z = a + bi y w = x + yi \)
Suma de números complejos: La suma se obtiene agrupando las partes reales y las partes imaginarias:
\( z + w = (a + bi) + (x + yi) = (a + x) + (b + y)i \)
También puede representarse como el par ordenado:
\( z + w = (a + x, b + y) \)
Resta de números complejos:
La resta se realiza de forma similar, restando parte real con parte real y parte imaginaria con parte imaginaria:
\( z - w = (a - bi) - (x - yi) = (a - x) - (b - y)i \)
También puede representarse como el par ordenado:
\( z - w = (a - x, b - y) \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Si \( z=6−3i \) y \( w=2+5i \), ¿cuál es el resultado de \( z + w \)?
Solución:
\( z + w = (6 − 3i) + (2 + 5i) = (6 + 2) + (−3 + 5)i = 8 + 2i \)
1. Si \( z=-7+4i \) y \( w=3+6i \), ¿cuál es el resultado de \( z-w \)?
Solución:
\( z-w = (-7+4i) - (3+6i) = (-7-3) + (4-5)i = -10-2i \)
Conjugado de un número complejo
Dado el número complejo \( z = a + bi \), el conjugado de \( z \) se denota por \( z \), con \( z = a - bi \)
Ejemplos:
| Número complejo | Número conjugado |
|---|---|
| \( z_1 = 5 + 2i \) | \( \overline{z_1} = 5 + 2i \) |
| \( z_2 = -3 - 4 \) | \( \overline{z_2} = -3 - 4 \) |
| \( z_3 = 0 + 7i \) | \( \overline{z_3} = 0 + 7i \) |
| \( z_4 = -6 + 0i \) | \( \overline{z_4} = -6 + 0i \) |
Multiplicación de números complejos
Dados los números complejos z = a + bi y w = x + yi, se define:
\( z w = (a + bi)(x + yi) = (ax - by) + (ay + bx)i \)
EJERCICIOS
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. El producto de \( z = 1 + 2i \) con \( w = 3 − i \) es:
Solución:
\( z⋅w = (1 + 2i)(3 − i) \)
Aplicamos la multiplicación:
\( =(1)(3)+(1)(−i)+(2i)(3)+(2i)(−i) \)
\( =3−i+6i−2i^{2} \)
\( =3+5i−2(−1)=3+5i+2=5+5i \)
Recordando que \( i^{2} = -1 \)
2. El producto de \( z = -2 + i \) con \( w = 4 + 3i \) es:
Solución:
\( z⋅w = (-2+i)(4+3i) \)
Aplicamos la multiplicación:
\( =(−2)(4)+(−2)(3i)+(i)(4)+(i)(3i) \)
\( =−8−6i+4i+3i^{2} \)
Recordando que \( i^{2} = -1 \)
\( =−8−2i+3(−1)=−8−2i−3=−11−2i \)
División de números complejos
Dados los números complejos \( z = a + bi y w = x + yi \), se define:
\( \frac{z}{w} = \frac{a+bi}{x+yi} = \frac{ax+by}{x^{2}+y^{2}} = \frac{bx+ay}{x^{2}+y^{2}}i \)
EJERCICIO
INSTRUCCIÓN: Lee atentamente cada pregunta y elige la respuesta correcta.
1. Si \( z = 3 - 2i \) y \( w = 1 + 4i \), ¿cual es el resultado de \( \frac{z}{w} \)?
Solución:
\( \frac{z}{w} = \frac{3+2i}{1+4i} \)
Multiplicamos numerador y denominador por el conjugado del denominador:
\( =\frac{(3+2i)(1+4i)}{(1+4i)(1+4i)} \)
Desarrollamos numerador y denominador:
\( (3)(1)+(3)(4i)+(2i)(1)+(2i)(4i)=3+12i+2i+8i^{2} \)
\( =3+14i+8(−1)=3+14i−8=−5+14i \)
Denominador:
\( (1)^{2} − (4i)^{2} = 1 − 16(−1) = 1 + 16 = 17 \)
Entonces:
\( \frac{z}{w} = \frac{-5+14i}{17} = \frac{5}{17} + \frac{14}{17}i \)





